RMS抖動計算Pk-Pk抖動
發布時間:2018/5/26 9:55:46 訪問次數:6635
- 51電子網公益庫存:
- YQR100R060
- ZMOT0BHH1A0CG
- ZSBG323671
- XL203A-3486
- V22B
- USX1862
- ACS709LLF-6BB-T
- S22P025S05
- H3LIS331DLTR
- OAA160S
- TFPT0603L1000JZ
- 01M2251SFC3
- 3006-1576-101-G100
- KT103J2
- NB12K00103JBB
抖動是實際信號的一組邊沿與理想信號之間的偏差(兔子:說白了,抖動就是實際情況和理想情況不一樣,差別越大抖動越大)。時鐘信號的抖動通常由系統中的噪聲或其他干擾因素引起。影響因素包括熱噪聲、電源變化(波動)、負載的狀況(負載也可以反過來影響時鐘信號)、設備噪聲和臨近電路耦合進來的干擾。http://new.yax360.com
抖動可以通過許多方式測量(不同方式測量到的抖動被分別加以定義),以下是主要的抖動分類:
周期抖動是時鐘信號的實際周期長度與理想周期長度之間的偏差,測量樣本為數目不定(隨機)的一組周期。如果給定一定數目的單個時鐘周期,我們就可以通過測量每個周期的長度并計算平均的周期長度,以及這些時鐘周期的標準差和峰峰值(peak-to-peak value)。這里所說的標準差和峰峰值也分別被稱為rms抖動和pk-pk周期抖動。
許多文獻將周期抖動直接定義為被測時鐘周期與理想周期之間的誤差。但是真實情況下很難對理想周期進行量化。如果我們用示波器觀察一個標稱100mhz的晶振,測得的平均時鐘周期卻可能是9.998ns,而不是理想的10ns。所以退而求其次,通常將平均周期作為理想周期看待(兔子:因為實際周期都是在理想值周圍按照一定規律分布的,如果測量時間足夠長,得到的平均值就可以非常接近理想值)。
周期抖動對于計算數字系統的時序裕量十分有用。假設在一個基于微處理器的系統中(上升沿采樣),處理器要求1ns的數據建立時間(即數據需要在時鐘上升沿1ns前保持穩定有效)。當時鐘的某個周期抖動為-1.5ns時,上升沿會出現在數據有效之前,如此處理器將會采集到錯誤的數據。http://new.yax360.com
類似的,如果另一個處理器需要2ns的數據保持時間,但是時鐘某一個周期的抖動是+1.5ns,那么實際有效的數據保持時間只有0.5ns,處理器也會采到錯誤的數據。
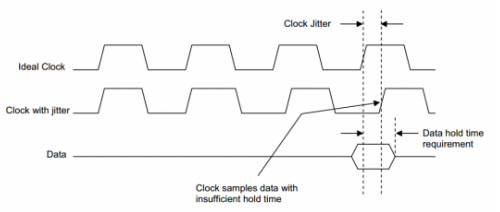
由于時鐘的周期抖動是隨機的,并遵循高斯分布。因此周期抖動完全可以用統計學中的均方根(rms ,root mean square,別說不會算)來表示,單位為皮秒(ps)。但是呢,峰峰值卻和計算建立保持時間裕量有更大的聯系(峰峰值表示了最大誤差,超過建立保持時間要求,數據采樣就有可能出錯)。 由高斯概率密度函數表(pdf ,gaussian probability density function)推導出來的。比如當樣本個數為100時,從統計學的平均情況來講,其中 99個會落在有效值周圍的±2.327σ范圍內,只有1個會落在該范圍之外。根據jedec標準的要求,某司測量rms周期抖動時設定的樣本數為10000。
jedec standard 65b中將周期抖動定義為某一隨機數量的時鐘周期與理想周期之間的偏差(由定義了一次,生怕大家忘了)。jedec標準進一步地指定了測周期抖動需要測量10000個信號周期(多一個少一個應該也無所謂吧)。某司推薦的測試步驟如下:
1. 測量一個時鐘周期(一個上升沿到下一個上升沿之間)的長度,即一個樣本
2. 等待隨機個時鐘周期http://new.yax360.com
3. 重復1、2兩步10000次
4. 通過測到的10000個樣本,計算平均值,標準差(σ),和峰峰值
5. 重復1-4步驟25次,通過這25組結果,計算平均峰峰值
10000個隨機樣本計算出的標準差(σ),即均方根(rms,也有人認為均方根和標準差并非等同)已經很精確了,rms的誤差可以通過如下等式計算:
樣本數為10000,rms誤差為0.0071 σn。這種誤差是隨機的,并且遵從高斯分布,通常用±3 x rms誤差來計算最大測量誤差。
又例如:如果從10000個樣本中計算出rms為10ps,則rms誤差為0.071ps,所有rms值都會落在10 ± 0.213ps(rms ± 3 x rms誤差)的范圍內。在實際應用中,若只有10000樣本,rms誤差可以忽略不計。http://new.yax360.com
來源:eefocus
- 51電子網公益庫存:
- YQR100R060
- ZMOT0BHH1A0CG
- ZSBG323671
- XL203A-3486
- V22B
- USX1862
- ACS709LLF-6BB-T
- S22P025S05
- H3LIS331DLTR
- OAA160S
- TFPT0603L1000JZ
- 01M2251SFC3
- 3006-1576-101-G100
- KT103J2
- NB12K00103JBB
抖動是實際信號的一組邊沿與理想信號之間的偏差(兔子:說白了,抖動就是實際情況和理想情況不一樣,差別越大抖動越大)。時鐘信號的抖動通常由系統中的噪聲或其他干擾因素引起。影響因素包括熱噪聲、電源變化(波動)、負載的狀況(負載也可以反過來影響時鐘信號)、設備噪聲和臨近電路耦合進來的干擾。http://new.yax360.com
抖動可以通過許多方式測量(不同方式測量到的抖動被分別加以定義),以下是主要的抖動分類:
周期抖動是時鐘信號的實際周期長度與理想周期長度之間的偏差,測量樣本為數目不定(隨機)的一組周期。如果給定一定數目的單個時鐘周期,我們就可以通過測量每個周期的長度并計算平均的周期長度,以及這些時鐘周期的標準差和峰峰值(peak-to-peak value)。這里所說的標準差和峰峰值也分別被稱為rms抖動和pk-pk周期抖動。
許多文獻將周期抖動直接定義為被測時鐘周期與理想周期之間的誤差。但是真實情況下很難對理想周期進行量化。如果我們用示波器觀察一個標稱100mhz的晶振,測得的平均時鐘周期卻可能是9.998ns,而不是理想的10ns。所以退而求其次,通常將平均周期作為理想周期看待(兔子:因為實際周期都是在理想值周圍按照一定規律分布的,如果測量時間足夠長,得到的平均值就可以非常接近理想值)。
周期抖動對于計算數字系統的時序裕量十分有用。假設在一個基于微處理器的系統中(上升沿采樣),處理器要求1ns的數據建立時間(即數據需要在時鐘上升沿1ns前保持穩定有效)。當時鐘的某個周期抖動為-1.5ns時,上升沿會出現在數據有效之前,如此處理器將會采集到錯誤的數據。http://new.yax360.com
類似的,如果另一個處理器需要2ns的數據保持時間,但是時鐘某一個周期的抖動是+1.5ns,那么實際有效的數據保持時間只有0.5ns,處理器也會采到錯誤的數據。

由于時鐘的周期抖動是隨機的,并遵循高斯分布。因此周期抖動完全可以用統計學中的均方根(rms ,root mean square,別說不會算)來表示,單位為皮秒(ps)。但是呢,峰峰值卻和計算建立保持時間裕量有更大的聯系(峰峰值表示了最大誤差,超過建立保持時間要求,數據采樣就有可能出錯)。 由高斯概率密度函數表(pdf ,gaussian probability density function)推導出來的。比如當樣本個數為100時,從統計學的平均情況來講,其中 99個會落在有效值周圍的±2.327σ范圍內,只有1個會落在該范圍之外。根據jedec標準的要求,某司測量rms周期抖動時設定的樣本數為10000。
jedec standard 65b中將周期抖動定義為某一隨機數量的時鐘周期與理想周期之間的偏差(由定義了一次,生怕大家忘了)。jedec標準進一步地指定了測周期抖動需要測量10000個信號周期(多一個少一個應該也無所謂吧)。某司推薦的測試步驟如下:
1. 測量一個時鐘周期(一個上升沿到下一個上升沿之間)的長度,即一個樣本
2. 等待隨機個時鐘周期http://new.yax360.com
3. 重復1、2兩步10000次
4. 通過測到的10000個樣本,計算平均值,標準差(σ),和峰峰值
5. 重復1-4步驟25次,通過這25組結果,計算平均峰峰值
10000個隨機樣本計算出的標準差(σ),即均方根(rms,也有人認為均方根和標準差并非等同)已經很精確了,rms的誤差可以通過如下等式計算:
樣本數為10000,rms誤差為0.0071 σn。這種誤差是隨機的,并且遵從高斯分布,通常用±3 x rms誤差來計算最大測量誤差。
又例如:如果從10000個樣本中計算出rms為10ps,則rms誤差為0.071ps,所有rms值都會落在10 ± 0.213ps(rms ± 3 x rms誤差)的范圍內。在實際應用中,若只有10000樣本,rms誤差可以忽略不計。http://new.yax360.com
來源:eefocus
下一篇:NPN硅三極管管腳的判別
 熱門點擊
熱門點擊
- 不對稱半橋式功率變換器
- 云計算市場分析與預測
- 供電電源的穩態直流精度
- DRAM 的市場需求強勁
- 新興產業為合肥經濟鍛造持久動力
- 中國開發服務器芯片可選的架構
- RMS抖動計算Pk-Pk抖動
- 高速緩存處理器宏單元的ARM720T
- 汽車正往微型化進化
- A12處理器的核心數和架構
 推薦電子資訊
推薦電子資訊
- iPhone5S/iPhone5C獲工信部認證
- 庫克一直看好中國市場的巨大潛力,并且自去年3月以來他已... [詳細]


 公網安備44030402000607
公網安備44030402000607





